秘密鍵から公開鍵を生成するアルゴリズム「楕円曲線暗号」

パブリックブロックチェーンにおける情報は、誰もが閲覧できることから、その秘匿性を担保することは非常に重要とされています。特にビットコインのようなお金に関わる情報の中身が簡単に分かってしまうことは避けなければなりません。それらの情報の暗号化のために公開鍵暗号方式を利用していることは、何度か述べています。そこで今回は、秘密鍵と公開鍵を結びつける重要な技術である「楕円曲線」を用いた暗号技術に関して紹介します。

秘密鍵・公開鍵

まず前提として秘密鍵と公開鍵について知っておく必要があります。秘密鍵は本人にしか分からない鍵で、公開鍵は秘密鍵と対になる一般公開される鍵です。ブロックチェーン技術においては、公開鍵暗号方式における秘密鍵と公開鍵を、「電子署名」と呼ばれるデータ送信者を確認するための方法として使用します。

ブロックチェーンのセキュリティに必要不可欠な鍵「秘密鍵・公開鍵」
ブロックチェーンの送金を支える技術「電子署名・マルチシグ」

それでは、秘密鍵と公開鍵はどのように作られているのでしょうか。まず秘密鍵に関しては、ランダムな大きい数字を適当に作成します。秘密鍵は本人にしか分からないことが前提なので、他人から見破られないことを深く考える必要はありません。

問題は公開鍵です。公開鍵は秘密鍵に何らかの計算を施すことで作成されるものですが、公開鍵はネットワークにブロードキャストされ、一般に公開されてしまう情報です。従って、公開鍵から簡単に秘密鍵を逆算されてしまわないように、計算方法に工夫を施さなくてはいけません。その計算アルゴリズムが、楕円曲線を利用した暗号化方式（楕円曲線暗号）です。

楕円曲線とは

楕円曲線とは次の形の方程式により定義される平面曲線です。

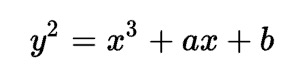
このa,bの値を変えることで、以下のように様々な曲線の形状になります。

しかしこの曲線は、明らかに楕円の形はしていません。「楕円」という言葉は、この楕円曲線はもう少し別のところから由来しています。この楕円曲線ですが、この後説明する暗号化のアルゴリズムに用いられています。また他分野では、数論の分野で重要とされており、フェルマーの最終定理の証明にも使用されています。

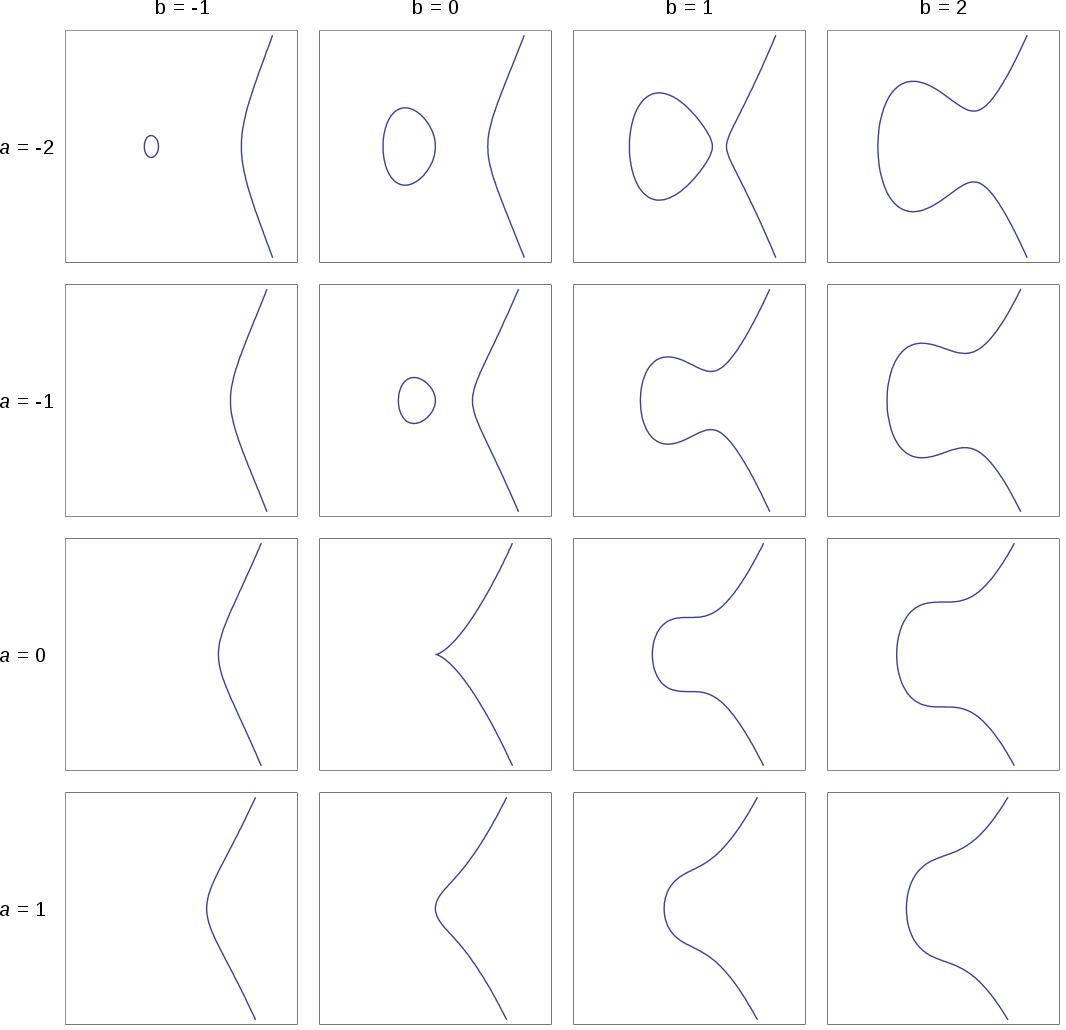
画像はウィキペディアの楕円曲線 から転載

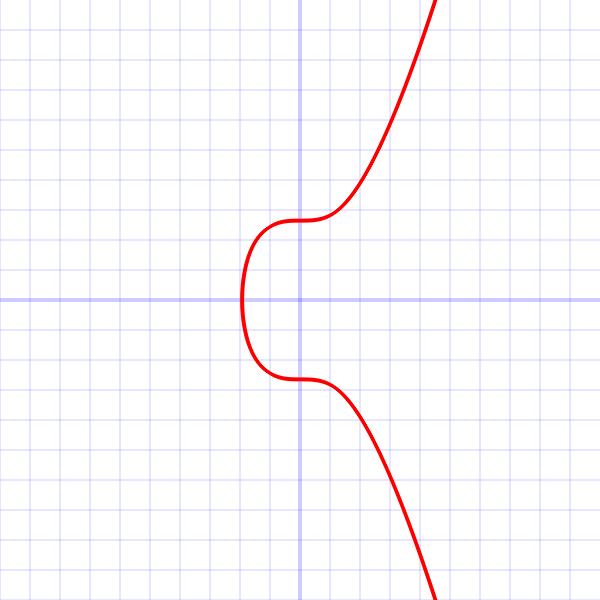
楕円曲線暗号による公開鍵の生成

ここからは、楕円曲線を用いた暗号化について説明します。まず、楕円曲線を用いて暗号化することを、楕円曲線暗号（Elliptic Curve Cryptography：ECC）と呼びます。ビットコインではこの暗号方式を用いることで秘密鍵から公開鍵を生成します。また楕円曲線暗号を使用して電子署名がされる一連の流れは「楕円曲線電子署名アルゴリズム」と呼ばれています。これはその名の通り、電子署名アルゴリズム（Digital Signature Algorithm：DSA）において楕円曲線暗号を用いるものであり、ビットコインの電子証明にも利用されています。

そして、楕円曲線暗号に使う楕円曲線の式は先程紹介した方程式に少し手を加えたものになります。

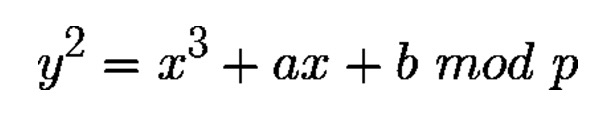
ここで、「mod p」という見慣れない式が出てきます。これは剰余演算（またはモジュロ）と呼ばれ、「a mod n」の場合、aをnで割った余りを指します。すなわち、上記の方程式は、左辺と右辺の余りが等しい方程式であると言えます。

具体的に、楕円曲線を使用してどのようにして秘密鍵から公開鍵を生成しているのでしょうか。手順としては少々複雑ですが、以下のように計算されます。

1. 楕円曲線のパラメータであるp,a,b、また基準点であるG(x,y)を決める
   • ビットコインで使っているSecp256k1でのパラメーターは以下の通り
     • a = 0x0000000000000000000000000000000000000000000000000000000000000000
     • b = 0x0000000000000000000000000000000000000000000000000000000000000007
     • p = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
     • Gx = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
     • Gy = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
2. Gに自身であるGを足し、2Gを求める（楕円曲線暗号における足し算）
3. 2.の行為をn回分（n：秘密鍵の値）繰り返すことで、値nGを得る
4. nGを公開鍵の値とする

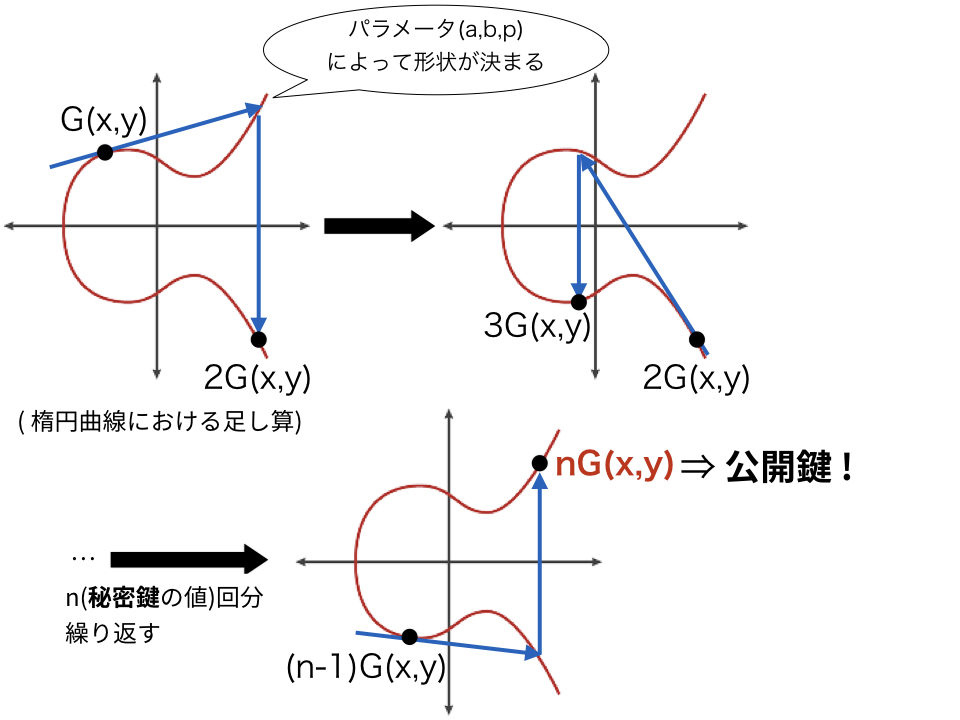
ここで、楕円曲線における足し算は通常の足し算・掛け算とは異なります。まず、ある楕円曲線上にある接点Gに関して、接線を得ることができます。この接線は必ず接点G以外の楕円曲線上の点と交わります。その交点のx軸対称の点が次の点2Gとなります。これを繰り返している様子が上図です。

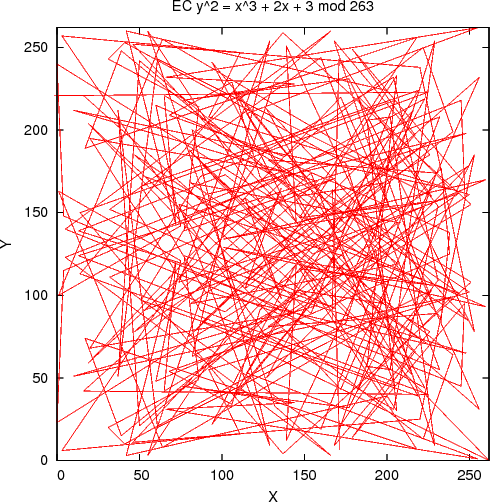
このように、ある点Gから何回も掛け算されてnGとなった軌跡の簡単な例が以下のように示されています。見ると分かる通り、軌跡の形は非常に複雑になっていますが、ある点Gからn回移動させた点nGを計算させることはコンピュータによって高速に計算を回すことで可能です。

ここで注目することは、ここまで見てきた楕円曲線の軸は、ある点(x,y)をpで割った余りとなっている点です。これはさきほどの方程式における「mod p」の部分が効いているためです。楕円曲線暗号のアルゴリズムは、点G及びpが分かった状態で、次の点を求める手順をn回繰り返してnGを求めます。数学的には、Gからn回剰余演算を繰り返してnGを求めることは簡単ですが、nが非常に大きい値の時にGとnGから剰余演算においてnを求めることは非常に困難であるとされています。これはハッシュ関数の性質と同じように一方向性があると言い、暗号の解読を不可能にさせるという点で強力なメリットとなります。こうしたことから暗号分野でよく利用されています。

画像：johannes-bauer.com

楕円曲線は数学的には少々難解な問題を扱っていますが、原理としては、自分の持つ秘密鍵からより安全な方法で公開鍵を生成するアルゴリズムです。このように普段は目にしない数学の力を使うことで、ビットコインを始めとしたブロックチェーンは安全性や秘匿性を担保されています。数学という観点からもブロックチェーンを学んでいくと、また一つ理解が深まるのではないでしょうか。