ブロックチェーンは様々な技術で構成されるシステムです。Peer-to-peer の通信技術やコンセンサスアルゴリズム、効率的にデータを格納するストレージを分散させるための分散ハッシュテーブルなど、上手に使いこなすにはそれなりに知識も必要でしょう。
今回は、その中でもブロックチェーンだけでなく、既存の様々なシステムで用いられているデジタル署名アルゴリズムについて基本となる概念について、主に工学的な観点から解説していこうと思います。
目次
前提となる知識
デジタル署名アルゴリズムは一般に広義の公開鍵暗号技術と暗号学的ハッシュ関数を用いて構成されています。したがってこの文章を読むにあたっては、これら 2 つに関する知識があると良いでしょう。
あえて「広義の」公開鍵暗号技術とした理由として、一般に「公開鍵暗号」と聞くと、RSA暗号のようなデータの機密性を担保する機能を持った暗号アルゴリズムをイメージしがちであるからです。厳密にはこれは違うのですが、この辺りをちゃんと説明しようとするとおおよそ 1 つのブログ記事の分量からかけ離れてしまいそうなのと、著者でも正確に説明できる自信がないので、今回は割愛します。気になった方は別の文献をあたって調べると良いと思いますが、この辺りの用語の説明についてはインターネット上にはかなり誤ったが多く散見するので、その辺は留意しておく必要があります。ともかくとして、ここでの広義の公開鍵暗号技術は対となる「秘密鍵」(署名鍵)と「公開鍵」(検証鍵)が存在する際に、数学上逆計算困難な問題を利用して、多項式時間内で公開鍵から秘密鍵を導出することが不可能である性質を持つ仕組みとしておきます。定義上ある程度の曖昧さはありますが、デジタル署名のおおまかな仕組みを理解する上では問題ないと思います。
また、ここで解説するのはあくまで暗号技術を用いたデジタル署名を対象とします。一般に、契約書の有効性を確かめる、などのユースケースを考えるときには技術ではなく国内法(いわゆる電子署名法)が参照されることになりますが、日本の国内法では、必ずしも暗号技術を用いたものが「電子署名」とされているわけではありませんので、これも混同に注意してください。この場合は電子署名法を参照するか、別途法律の専門家にご相談いただくのが良いでしょう、
デジタル署名アルゴリズムって何のためのもの?
デジタル署名とは、何のために存在するものでしょうか?この技術は一般に公開鍵暗号の原理と、暗号学的ハッシュ関数を用いて構成されていて、以下のような性質を持っています。
- 署名の検証に成功した場合、署名が作成・付与された時点から現在まで署名の対象となるメッセージに変更が加えられていないことを保証する(データ完全性)
- ある検証鍵(公開鍵)で署名の検証に成功した場合、その検証鍵と対となる署名鍵(秘密鍵)が確かにそのメッセージに署名したことを保証する(真正性)
- 署名が有効である限り、署名の作成者が署名を作成した事実を認めないことができないことを保証する(否認防止)
デジタル署名のアルゴリズムによっては他にも様々な性質があるかもしれませんが、大方この 3 つに関しては共通して持っていると考えて良いと思います。ただ、これではなんとなくお堅くて具体的なイメージを持てない方もいると思うので、ユースケースの 1 つとして契約書への署名に当てはめてみて考えてみましょう。
皆さんは、紙媒体であっても、電磁的な媒体であっても、契約書に「署名」するとき、あるいは「署名」を求めるとき、何を期待して「署名」を行いますか?
法的な構成要件が〜とか考え出すと大変なので、そのあたりは抜きにしても、大抵の場合は「私はこれこれの決まり事に対して、確かに確認して、同意しました。」といった事実を示すために行うと思います。したがって、署名をした後に悪い人がこっそりと、この「決まり事」の文章を変えてしまうと非常に困ったことになります。金 10000 円を支払う、と書いてあるところに 0 を付け足されて、「後から桁が 1 つ足りないじゃないか!」と指摘されるようなことがあったらたまりません。つまり、契約書の内容の改竄を防止する必要があるわけです。
また、せっかく合意したのにもかかわらず、「そんな契約書に署名した覚えはない!」と言われても困ります。この場合、2つのケースが考えられます。1つ目は、本当に署名したのが本人ではないケースです。実世界で紙に署名する時にはあまり想像のできないケースですが、例えばインターネットを介した通信では通信先が本当に期待した通信先であるかを目で見て確かめる手段はありません。したがって、署名されたメッセージを送ってきたのが本当に署名鍵の持ち主であると確認する必要があるわけです。2つ目のケースは、署名したのが本人であるのにもかかわらず嘘をついているケースです。したがって署名者がその署名をした事実を認めないことを防ぐ必要もあります。
こういったことを達成するために、紙媒体の場合はインクの滲み具合で判別するだとか、紙の契約書を 2 通用意しておいてその両方に署名し、割印を押して契約した上で当事者双方が保管するだとか、あるいは重要な物事の場合は公証役場に持っていき、公権力を根拠に認証してもらう、といったことを行います。最後の 1 つはさておき、前者2つの場合は電磁的な媒体で保管される場合は通用しません。なぜならデジタルデータはビット列のパターンでしかないため、複製が容易であり、偽造・改竄されたのか否かといったことが第三者の立場から判別つかないからです。もちろん、「紙媒体だって偽造できるじゃないか!」というご指摘もあるかもしれませんが、何せ難易度が違います。可能・不可能の話というよりは、程度の話だと捉えるとご理解いただけると思います。
デジタル署名アルゴリズムの仕組み
それでは先述したような性質をどうやって実現するのでしょうか?
一般に普及しているアルゴリズムでは、先ほどから何度も登場している(広義の)「公開鍵暗号技術」の原理と「暗号学的ハッシュ関数」を用いられることが多いです。一例として、最も古典的なアルゴリズムの 1 つである RSA 暗号の原理を用いたデジタル署名アルゴリズムの流れを紹介したいと思います。ただし、全てのデジタル署名アルゴリズムが同じ流れ・仕組みであるわけではないということに注意が必要です。むしろこの流れは RSA 暗号が持つ後述するある特徴を用いているわけですが、実はそのような特徴を持つ方が特殊であったりして、この流れもまた非常に原理的でありながら、特殊であるともいえると思います。実際、Ethereum や Bitcoin では、secp256k1 と呼ばれる楕円曲線上の楕円曲線署名アルゴリズム(Elliptic Curve Digital Signature Algorithm; ECDSA)を利用しており、これはこの先説明するような仕組みとは全く違った仕組みになります。そのため、あくまで一例として、こういう感覚で実現されているのだ、といったのを掴むためのものとして捉えていただけると幸いです。
RSA 暗号でのデジタル署名アルゴリズムを利用した署名・検証の流れを図にしたので、以下に示します。
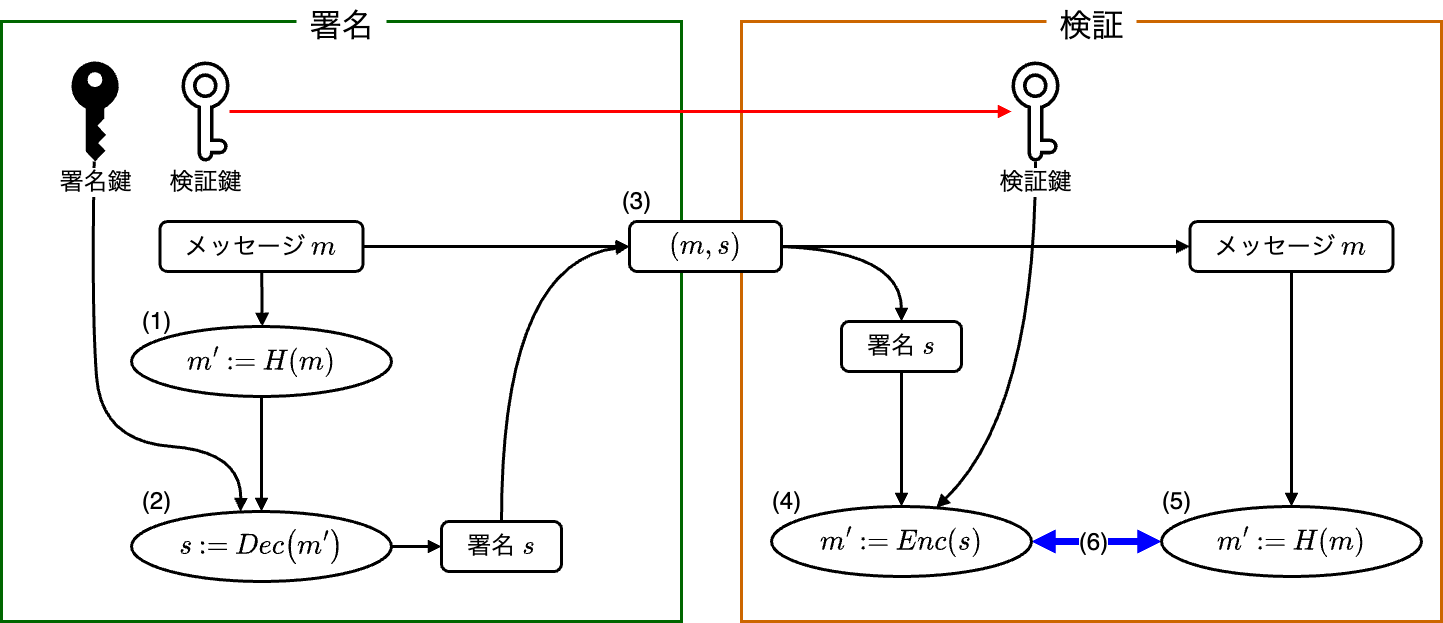
前提として、署名する対象となるメッセージを m、得られる署名を s、RSA暗号の秘密鍵で復号する関数を Dec、公開鍵で暗号化する関数を Enc 、任意の暗号学的ハッシュ関数を H とします。さらに前提として、RSA 暗号はメッセージを秘密鍵で復号して得られた符号を公開鍵によって暗号化することで元のメッセージに戻すことができる、という性質を持っており、これは s = Dec(m)、m = Enc(s) のように表せます。
署名の流れ
最初に署名の流れについて説明します。
- 署名するにあたって対象となるメッセージ m をハッシュ関数に渡して要約値 m’ を得ます (1)
- 次に、署名鍵(秘密鍵)を用いて復号の処理を行います (2)
- これが所謂「署名する」という行為にあたり、署名 s を得ることができます
- 最後に得られた署名 s と対象となるメッセージ m をセットにして、検証する相手に渡します (3)
署名するにあたって要約値を用いているのは、先に述べたようなデジタル署名に求める性質を満たすために全てのデータが必要なわけではなく、また RSA の署名は元となるデータに比してサイズが大きくなるためです。要約値を使うことで署名データのサイズを小さくすることができます。
検証の流れ
次に、署名されたメッセージに対する検証の流れについて説明します。
- 渡された署名とメッセージのセット (m, s) から署名 sを取り出し、予め入手しておいた検証鍵(公開鍵)を用いて暗号化の処理を行います (4)
- 渡された署名とメッセージのセット (m, s) からメッセージ m を取り出し、ハッシュ関数に渡して要約値 m’ を得ます (5)
- 最後に、(4) で得た値と (5) で得た値を比較して等しければ署名は有効であると確認できます (6)
以上が RSA 暗号によるデジタル署名アルゴリズムの署名と検証の流れです。仮に途中でメッセージのビット列が変わると、ハッシュ関数から得られる要約値が変わり、署名から得られる値と等しくならなくなるので、改ざんに気づくことができます。また、公開鍵と秘密鍵(検証鍵と署名鍵)は対となっているので、ある検証鍵での検証に成功するということは、対となる署名鍵で署名されたということがわかるわけです。
デジタル署名の注意点
便利なデジタル署名ですが、先の図を見ればいくつか気をつけるべきこともわかると思います。
第一に、検証するには予め検証鍵(公開鍵)を得ておく必要があります(図の赤矢印部分)。果たしてこれはどこから得るのでしょうか?インターネット上の通信を介して得る場合、この検証鍵自体が絶対に真正なものであると言えるでしょうか?第二に、検証鍵自体が正しいデータであって、仮に署名に検証としても、果たしてその持ち主が必ず自分の期待する人物(あるいは実体)であると言えるのでしょうか?
答えは必ずしもそうとは言えない、です。検証鍵(公開鍵)をインターネットなどの通信経路上で交換する場合、悪意ある第三者がその内容を書き換えてしまう可能性があります。一般には中間者攻撃などと呼ばれる攻撃です。また、仮にアルゴリズムとして正しい、検証に成功する検証鍵のデータを得ることができても、鍵ペアの持ち主が成りすました人物である可能性が当然あります。例えば、X(旧 Twitter)上で有名人を名乗るアカウントがあり、たまたま物好きなので、「私の電話番号はこれです!」と示していたとして、仮に電話が正しくつながったとしても、その先が本人であるとすぐに信じることはできないと思います。これと同様なことが検証鍵の交換に関しても言えるのです。
この問題を解決するためのアプローチとして、信頼の連鎖を利用した公開鍵基盤(Public Key Infrastracture; PKI)や Web of Trust といった概念が登場します。これらはブロックチェーンを活用する上でも知っておいて損はない概念となるのですが、ここまで説明すると長くなってしまうので割愛します。また機会があれば解説記事が書ければと思いますが、気になる方がいらっしゃれば調べてみてください。とは言え、デジタル署名だけでは現実世界の信頼に関わる問題全てを担保することはできないんだな、ということは理解できると思います。
ブロックチェーンでの応用
最後に、これらのデジタル署名アルゴリズムはブロックチェーンでどのように利用されているのでしょうか?
ブロックチェーンのシステムを動かすにあたって、ノードに送られてきたトランザクションのデータに対して、本当にアドレスと紐づくユーザがそのトランザクションを送ってきたのか、といったことなどを確かめる必要があります。そのため、ユーザは自分が持っている署名鍵(秘密鍵)を使ってトランザクションデータに署名を行ってから、署名とともにデータを送信するのです。具体的に例えると、「A さんから B さんに 1万円を送る」という操作をブロックチェーンに書き込むとして、本当にその操作が A さんによって送られたもので、その操作内容が途中で改ざんされていないか、を検証する手段として使われている、というわけです。
ブロックチェーンによって利用しているアルゴリズムは様々で、例えば先述した通り Ethereum や Bitcoin では secp256k1 と呼ばれる楕円曲線上の ECDSA のみを利用していますが、Polkadot では Schnorr 署名や EdDSA を用いることも可能とされています。
まとめ
今回の記事では、デジタル署名アルゴリズムの基本的な部分について、解説しました。これらの仕組みはブロックチェーンだけではなく、SSH や TLS での通信などインターネットの通信を安全にしたりするための仕組みや、単にデジタルの契約書や証明書などでも使われており、匿名の通信を要するサイバー空間での信頼を支える重要なものです。しかしながら、著者にとっては割とブラックボックス化されたり、あるいは誤って理解しがちな要素だと感じています。今回の解説が理解の一助となれば嬉しい限りです。




